Weathering Catastrophic Storms: the Science and Philosophy of Hurricane Prediction

The science of predicting hurricanes is crucial for disaster management and insurance, but also raises difficult methodological and philosophical questions. In this post, Joe Roussos asks whether hurricane modellers should average the results from different models of hurricane frequency.

The 2017 hurricane season is off to a disastrous start. When Harvey made landfall on Friday 24 August, it was as a category four hurricane; the strongest to hit Texas since 1961. The damage and disruption have been enormous, with over 70cm (30in) of rain in some areas. Fifty people have died, and with flooding worsening in major cities, the damage may well increase.

This post introduces some philosophical issues raised by hurricane science. As the fallout of Harvey will illustrate, hurricane predictions influence everything from disaster planning to whether homeowners are properly insured. Hurricane science therefore offers an important arena for the application of the philosophy of scientific models, the decision theory of severe uncertainty and the social epistemology of policy making in the face of disagreement. In my research I study these questions, working with weather scientists and their clients in the insurance industry. I‘m going to outline some of the issues I’ve encountered here, and for those interested in more detail I’ll link to two supplemental posts on my website.

My project builds on some of the LSE Department’s recent work on climate science, and connects to themes from the Managing Severe Uncertainty research project. The main question in the first phase of my research is how to deal with the significant level of disagreement over the factors influencing hurricane generation, which manifests itself in a variety of simulation models for predicting hurricane landfalls.

The science of hurricane prediction

For North Atlantic hurricanes, the models operate roughly as follows (this is a process closely governed by regulators such as the Florida Commission on Hurricane Loss Projection Methodology). At a high-level, each model’s aim is to calculate the probability that a hurricane of a given intensity will make landfall at a particular point on the Atlantic coast of North America. The coast is divided into regions, called “gates”, and a probability is calculated for each gate, for a given forecast year. This allows for local disaster planning  and the pricing of insurance premiums.

The models simulate hurricanes from their origin in the “main development region” (a central Atlantic basin where storms from West Africa typically develop into tropical cyclones), through to their dissipation; with most of the focus on whether and where they reach land. (Here is a great video of Harvey’s unusually late development into a hurricane in the Gulf of Mexico.)

The simulation is based on the historical database of hurricane landfalls from 1900 to today, called HURDAT2. For large hurricanes (category 3–5), there isn’t much data: fewer than 70 entries. This data gives us a statistical foundation for the model: from 1950 onward it provides details on the track each hurricane followed. This is used to generate many thousands of simulated hurricanes (using a statistical method, such as varying existing hurricane tracks along a random walk). By using a sample of these (statistical) storms that matches the frequencies observed in the full (HURDAT2) database, scientists create a dataset large enough to work with.

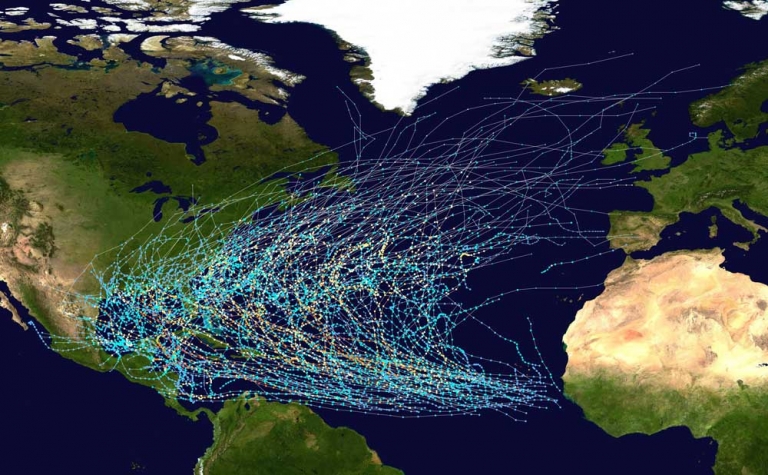
A “track map” showing the paths of all North Atlantic Hurricanes from 1980 to 2005.
Public Domain.

A set of initial questions – questions we have not yet begun to investigate – already emerges:

• First, what is the impact of having a regulator governing the formulation of scientific models? The state’s duty to protect consumers by governing insurance providers butts up against the ordinary process of scientific discussion and debate, and forces insurers to use an externally provided view of risk.

• Second, how should we regard this statistically generated dataset? It cannot count as “evidence” in the same way observations do, but it seems to offer scientists more than the limited observation data. But if the real data is too sparse to allow us to generate reliable probabilities from frequencies, why can we rely on probabilities generated from such a statistical dataset?

A storm of words

A number of scientific debates complicate any attempts to implement the recipe described above, and improve on mere historical frequency data.

First, there is a debate about which data should be included: just direct reports of landfall, or also more recently available data on storm formation in the Atlantic basin. The basin data tells us more about the physics of storm formation, and about potential hurricane tracks, but covers a shorter time period. Landfall data tracks the impact we care about directly, and has a longer history.

Second, there is a debate about the drivers of hurricane formation. Tropical storms use heat energy from the ocean surface to develop into hurricanes (basically, warmer sea water leads to more evaporation), meaning that sea-surface temperature is one of the major contributors to the generation of tropical storms. Modellers of North Atlantic hurricanes disagree on whether to focus their models on temperatures in the central Atlantic basin, or to include the influence of Indo-Pacific sea-surface temperatures.

A third debate is whether a flip has recently occurred in the long-term oscillation of sea-surface temperatures. These temperatures appear to oscillate naturally, and the multi-decade oscillation in the Atlantic is one of the most important inputs to modelling North Atlantic hurricanes over multiple years. The NOAA explain the impact: “during warm phases of the [Atlantic multi-decadal oscillation], the numbers of tropical storms that mature into severe hurricanes is much greater than during cool phases, at least twice as many.” So, this debate is about whether we should expect far fewer hurricanes in the near future.

These and other debates mean that, if one were to model each of the major views, on each debate in the literature, one would end up with about 20 different models of hurricane formation and landfall along the North American Atlantic coastline. What should policymakers do in the face of such disagreement?

Averaging in the face of uncertainty

Suppose we collect all 20 models described above. Each will likely generate different landfall rates (for a given category of hurricane) for any single gate. How should we choose which one to follow? These different rates would lead to different insurance premiums, different resource trade-offs when investing in flood defences, and so forth.

Philosophers have studied a very similar problem: expert disagreement. One thread of that debate, often associated with Alvin Goldman, is about whether non-experts can successfully choose between disagreeing experts (or, in our case, choose which model to use). Another thread, which I will pick up here, is about how to use all of the available opinions to form a “best” estimate.

A popular approach is to combine the different answers and use the average. This is widely advocated for in the forecasting literature, and is common practice amongst climate scientists, when modelling climate change and hurricanes.1

Imagine that you have to guess how many sweets are in a jar. You find three sweet-jar experts, and they give you three answers: 100, 108, 113. If you trust each expert equally, then the average of their guesses is 107. Many think that this should be your guess. The hope is that by averaging you cancel out the errors in each expert’s opinion.

Popularity aside, there are significant philosophical concerns with averaging. For one thing, it is not compatible with Bayesianism. But, leaving that aside (Bayesianism is a demanding taskmaster), there are significant further problems.

In the case of models, it is common to try and assess which does best against questions with known answers, and then to weight each model’s output according to its predictive skill. There are different ways of calculating these skill scores, but many use “hindcasting”: the historical data is divided into two periods, say 1950-1999 and 2000-2005. The model is trained on data from the first period, and then tested on its prediction of the hurricane landfall frequency for the second period.

Hindcasting comes with a range of methodological decisions. The length of the test period can be varied; one can choose to hindcast against the most frequent period, or against a whole series of periods in the past; if testing against a series of periods, we can count each equally or weight the recent past more. Such questions arise for (almost) any scoring rule, and can significantly influence the result.

Additionally, a range of scoring rules exist for measuring predictive skill. The Australian Bureau of Meteorology maintains a website on techniques for scoring probabilistic forecasts.2 It lists seven categories of forecast, and covers more than 50 scoring rules, visualisation techniques and analytical approaches to measure forecasting success. Some are appropriate only for a single category, others have broader application.

Philosophical responses

Which rule to use in what case is itself a matter of expert debate, and so on pain of introducing a second decision-problem for our policy-maker, we cannot easily devise a method for them to select a single rule. The philosophers’ favourite, the Brier score, will help you select a single model, but is of little use in generating weights for an average that can separate out models with very different performances. My belief – expanded upon in this post – is that, inevitably, the choice of skill score will be pragmatic, and introduce an avenue for non-scientific values to influence the result.

A more radical proposal is to embrace the uncertainty of the modelling process. David Stainforthargued in a series of co-authored papers in 2007 that climate models are so uncertain that no individual model’s central predictions should be taken seriously. (See this post for more details on that argument.)

Some structural similarities, and causal interactions, imply that hurricane models should be treated similarly. As global warming advances, these models increasingly simulate a never-before-seen state of the climate system. The very hypothesis of climate change motivates against the use of hindcasting: skill at reproducing the past will not predict the future, unless we have a strong handle on the “forcing scenario” – such as the degree of warming to expect – which we do not. Hurricane models are also beset by issues of known inadequacies in the models, with unknown effects. The tiny initiating dataset leads to a form of initial condition uncertainty arguably as severe as in the climate case. These are all key ingredients in Stainforth’s argument about climate change models.

Stainforth’s conclusion in the case of climate models is that “today’s ensembles give us a [only] lower bound on the maximum range of [our] uncertainty.” Lower bound, note, because as we come to understand the uncertainties in our models we expect the uncertainty in the result to increase. Instead of attempting to use any single prediction, Stainforth and his co-authors recommend considering all outcomes that any model considers possible. Rather looking for the expected scenario and planning for that, we should recognise that current science tells us that all of these outcomes are possible, and, crucially, that it cannot tell us anything more than that.

Such an approach makes some decisions harder: it offers no easy way for insurers to calculate their capital requirements, or to set premiums. But if the current, convenient, landfall rates cannot be justified then we need insurers to be more cautious, rather than relying on a misleading average.

Joe Roussos is a PhD student in LSE’s Department of Philosophy, Logic and Scientific Method. He is interested in social aspects of science, and his work involves philosophy of science, social epistemology and decision theory. His thesis concerns decision-making about highly uncertain sciences (like hurricane prediction) by non-expert policymakers. This post first appeared on the LSE's Philosophy, Logic and Scientific Method blog. 

Photo Credit: NASA Goddard Space Flight Center Via Flckr (CC BY 2.0)